どのような色でも、式(2.1)に示すように、3つの原色(R)、(G)、(B)の加法混色によって
等色できることが確認されています。
C(C) ≡ R(R) + G(G) + B(B) ・・・(2.1)
特定の色刺激R、G、Bを定め、その混合量を明示することによりあらゆる色光を表現
することができます。
色刺激R、G、Bは互いに独立で、このうち2つを加法混色しても残りの1つの色とは
等色できません。
このような色刺激を原刺激と言います。
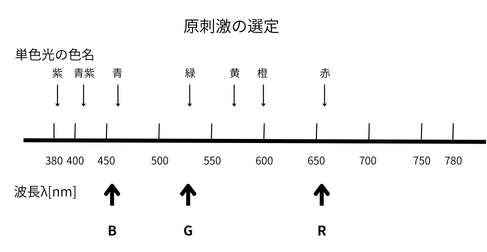
原刺激は、現在は以下の様な波長に選定されています。
原刺激
R:波長700[nm]の単色光
G:波長546.1[nm]の単色光
B:波長435.8[nm]の単色光
GとBは水銀の輝線スペクトルです。
原刺激の選定
原刺激の選定は、等色実験時にできるだけ多種の色光に対して原刺激の加法混色だけで
行いたい。
⇩
等色されるテスト色光の方に原刺激を加えることは避けたい。
⇩
可視スペクトルの中央と両端に近く、かつ鮮やかに見える色の波長を選択することに
なります。 です。Rは後に700[nm]になります。
です。Rは後に700[nm]になります。
明度係数と三刺激値
原刺激の量は輝度などの測光量をそのまま用いることはできません。
人の色感覚の特性は、色あいと明るさが比例しないためです。例えば青い色は暗い
にも拘らず色あいに関しては鮮やかさを強く感じます。
⇩
R、G、Bは光の強度(明るさ)に対して何らかの補正が必要です。
⇩
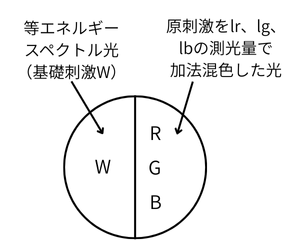
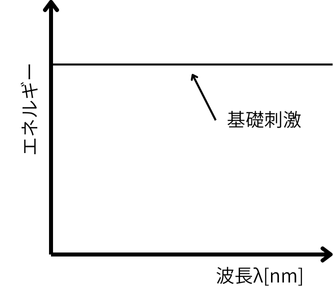
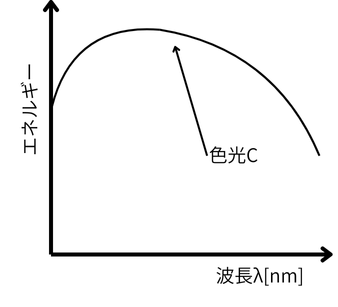
補正の基準として、一般に等エネルギースペクトルの白色光を用います。
⇩
⇩
原刺激の明るさを調整して加法混色し、等エネルギースペクトルの白色と等色させ
ます。等エネルギースペクトルの白色を基礎刺激といいます。
⇩
この時の原刺激のそれぞれの測光量(輝度)をlr、lg、lbとします。
⇩
また、色光Cに原刺激の明るさを調整して加法混色して等色させた場合の原刺激の
それぞれの測光量(輝度)をLr、Lg、Lbとします。
⇩
原刺激R、G、Bの量を表現する単位を、等エネルギースペクトルの白色を基準に
すれば、原刺激の量R、G、Bは以下のように表せます。
⇩
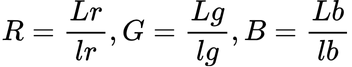 ・・・(2.2)
・・・(2.2)
⇩
lr、lg、lbを明度係数、その基準となる等エネルギースペクトルの白色刺激を
基礎刺激と呼びます。
⇩
このようにして得られたR、G、Bは人の白色に対する感覚を基準にした原刺激
の量であると言えます。
⇩
このR、G、Bを三刺激値と呼びます。
⇩
等エネルギースペクトルを持つ白色に対する三刺激値は
R=G=B
となります。
⇩
三刺激値という原刺激の量を表す単位によって、任意の色光を(2.1)式の形で
定量的に表色することができます。
式(2.1)と式(2.2)より、任意の色光(C)の輝度をLcとすると、加法混色された
色の輝度は各原刺激の輝度の和ですから、
Lc = Lr + Lg + Lb ・・・(2.3)
すなわち
Lc = lrR + lgG + lbB ・・・(2.4)
とあらわされます。
三刺激値は計測された光の明るさである輝度ではありません。輝度を明度係数
で割ることにより出てくる新しい数値、色の強さを表すために生み出された新しい
数値です。
例えば、原刺激R、G、Bを同じ比率の三刺激値で混色すると白色になるように
決められた色専用の単位です。
lr=1、lg=4.5907、lb=0.0601の比率で原刺激R、G、Bを加法混色すると白色に
なるということが実験で確かめられています。
1/lr、1/lg、1/lbを原刺激の単位にとると、明度係数lr、lg、lbは原刺激を用いて
色光Cに等色した時のそれぞれの測光量Lr、Lg、Lbを色表示のための量(三刺激値)
に変換するための係数と考えられます。

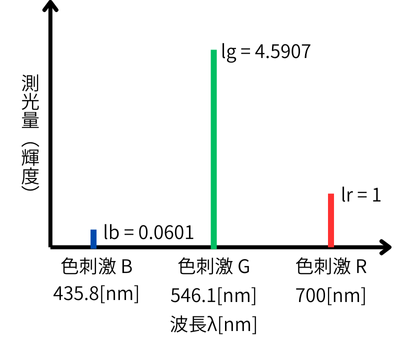
原刺激の測光量を、等エネルギースペクトルに等色した場合の測光量(lr, lg, lb)
で補正して、R=Lr /lr, G=Lg/lg, B=Lb/lbとする。
このR、G、Bを三刺激値といいます。
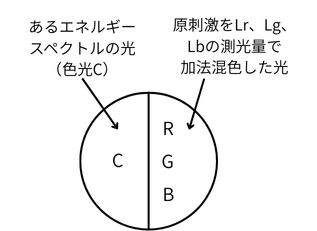
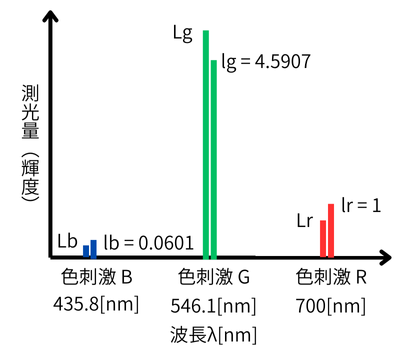
色度座標
R、G、Bを3次元軸にとり、色光Cをベクトルで表現すると以下の図-2.1の
様になります。
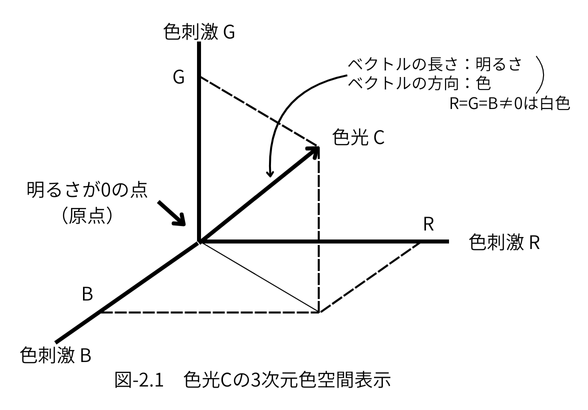
上図は C≡R・R + G・G + B・B の3次元表示です。
R、G、Bの三刺激値が各色刺激のベクトル長と考えると、
明度係数の逆数 1/lr、1/lg、1/lb が各色刺激の単位ベクトルと
なります。
以下の図-2.1の様に座標(1, 0, 0), (0, 1, 0), (0, 0, 1)の3点を頂点とする
正三角形の平面(単位平面または1-1-1の面)を考えます。
⇩
色光Cの色はベクトルの方向の違いだけなので、上記単位平面を
ベクトルが横切る座標で表現すると色の違いだけを表すことができて
便利です。(三刺激値で色光を表すと、色光の色だけでなく、強度も
合わせて表現してしまう)
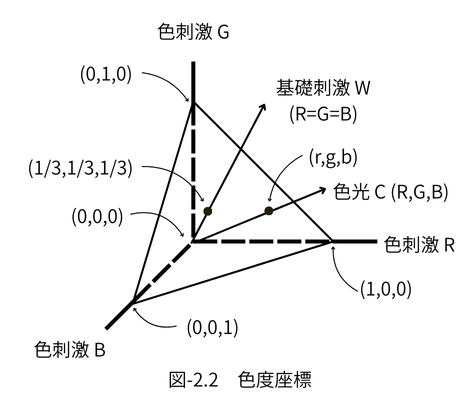
色光Cの色合いは単位平面を横切る座標(r, g, b)で表色されます。
この座標を色度座標といいます。色度座標は小文字で記します。
上記の単位平面と色光ベクトルCの座標をr, g, bとすれば、次の関係が
成り立ちます。R、G、Bは三刺激値です。
![]() ・・・(2.5)
・・・(2.5)
r, g, bは色光の強度の情報を持たず色だけの情報を表すため、色度座標
といいます。上記3次元空間を刺激値空間といいます。
r + g + b = 1 の関係があるため、色光Cはr, g, bのどれか2つで表色
できます。一般にrとgを用いて表色します。(図-2.3)
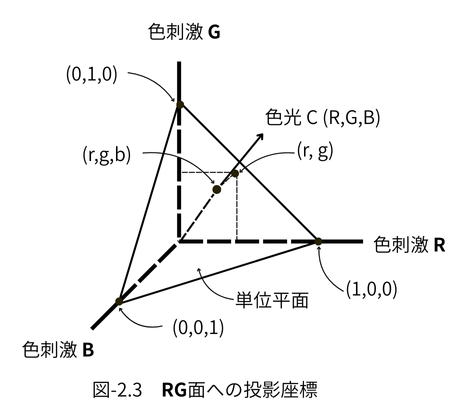
単位平面上の座標(r, g, b)には r + g+ b = 1 の関係があります。
このため色光Cの色合いを表す色度座標としてはRG面への投影座標
(r, g)によって色度座標は決まります。
色度はR、G、Bの三刺激値の割合であり、色の三属性から明度を除いた、色相と彩度を
表すものです。
等色実験
ライトとギルドという2人の研究者が行った等色実験は、CIEがRGB表色系とXYZ表色系
を定める基になりました。以下に2人の実験装置と結果を示します。
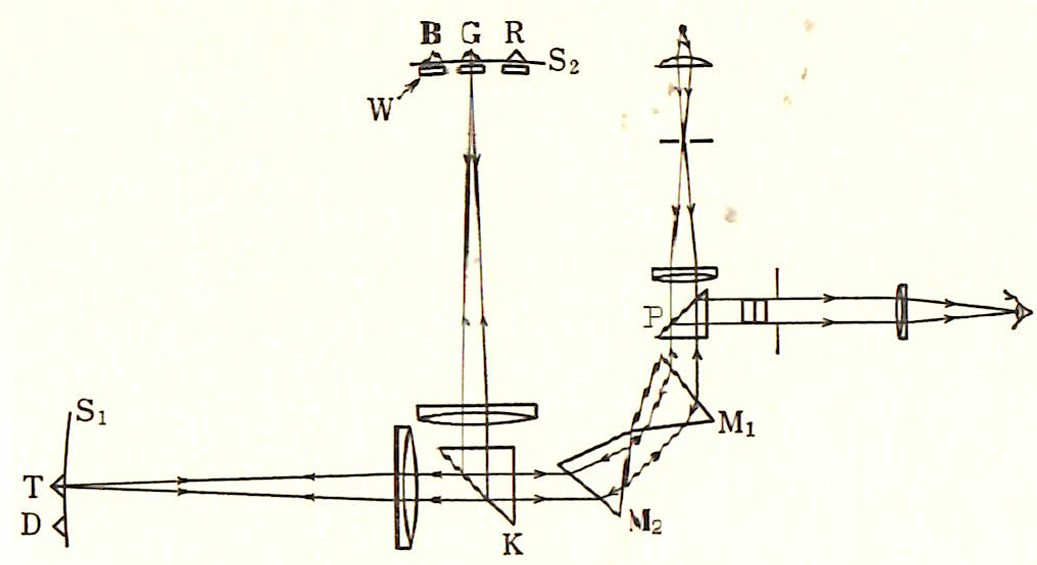
図-2.4 ライトの色彩計(池田光男 色彩工学の基礎 朝倉書店(1980))
器械原刺激にはモノクロメータによる単色光を使用しています。
光源から出た光は分校用プリズムM1、M2を通り、プリズムKによって、図では
上方へ曲げられ、S2の面にスペクトルを構成します。そこには3つの小さな全反射
型プリズムR、G、Bが、それぞれ650[nm]、530[nm]、460[nm]の位置に置かれて
おり、これらの波長の光のみが反射されて元きた方向へ戻り、プリズムK、分光プ
リズムM2、M1を経てプリズムPによって観測者の眼に入ります。
プリズムM2、M1を経たこれらの器械原刺激は完全に混合されており、1辺2°の
正方形の二分視野の片方を形成します。
他方、プリズムKで曲げられないで、図では左の方へ行った光はS1面にスペクトル
を構成し、そこの波長λの位置に置かれた全反射プリズムTによって反射された波長
λの光のみが元来た方向へ戻り、プリズムPによって観測者の眼に入ります。
これが二分視野のもう一方を形成しテスト刺激となります。
S1面に置かれたもう一つの全反射型プリズムDは、テスト刺激の彩度を落とすため
のもので、その位置は三つの原刺激のどれか一つと同じ波長の位置になります。
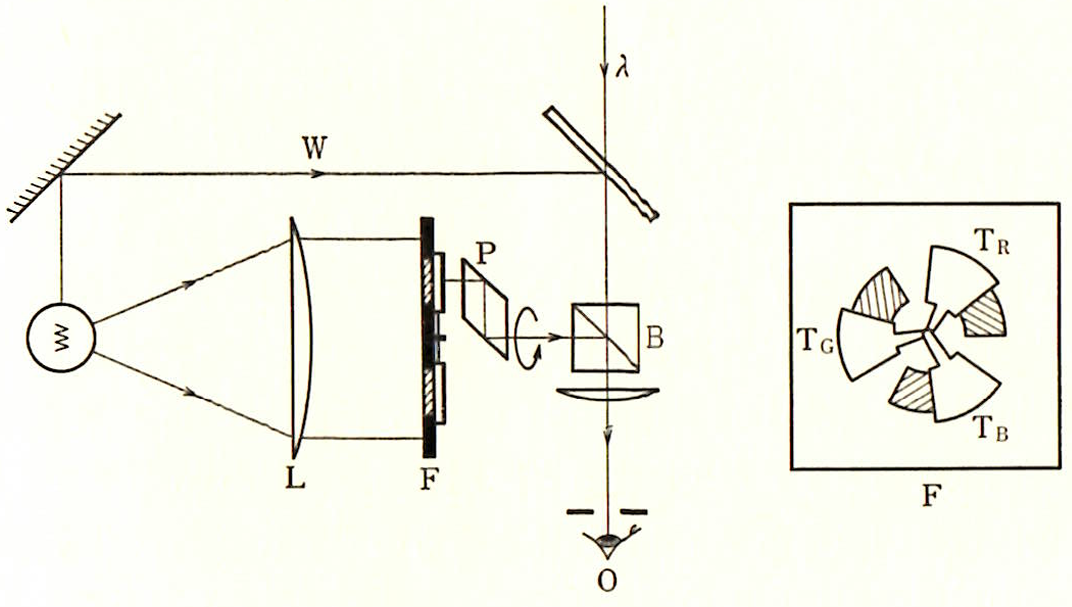
図-2.5 ギルドの色彩計(池田光男 色彩工学の基礎 朝倉書店(1980))
白熱電球からの光をコリメータレンズLで平行光にした後、R、G、Bの色フィルタ
でできた3つの窓を持つF面に当てます。3つの窓は挿入図に示すように円周上に並べ
られ、それをシャッターTr、Tg、Tbが部分的に覆っています。これらはそれぞれ独立に
円周上に動かすことができ、窓を通る光量つまりはR、G、Bの原刺激の量を変えること
ができます。窓の後部には光軸を軸に回転するプリズムPがあり、これが原刺激R、G、
Bを速い速度で順次観測者の眼に送り、時間的に混色させます。これにより、2°の
大きさの二分視野の片方が出来上がります。
もう一方のテスト刺激の視野は、モノクロメータから出た波長λの単色光がビーム
スプリッタBを通って眼に入ることにより形成されます。
観測者Oは2°視野のほぼ中央を見ながら二分視野の二つの色を見比べ、それらが完全
に同じになるようにシャッタTr、Tg、Tbを調節します。
しかしながら単色光の色は非常に鮮やかなため、3つのシャッタをどう調節しても
等色しない場合が多くあります。この時はテスト刺激の鮮やかさを弱めて等色を実行
しています。ギルドは白熱電球からの白色光Wをそれに用いました。
この時の等色方程式は、
![]() ・・・(2.6)
・・・(2.6)
と記述でき、以下のようになります。
![]() ・・・(2.7)
・・・(2.7)
ここでC(W)が
![]() ・・・(2.8)
・・・(2.8)
であれば、
![]() ・・・(2.9)
・・・(2.9)
となり、単色光λの色が3つの原刺激で表わされます。
ギルドの器械原刺激は色フィルタによるもので、単色光ではありません。しかし
各原刺激は三つの単色光の原刺激の適当な和によって置き換えられるので、データを
とってから計算によって単色光の原刺激へ変換することができます。
2人の研究者が等色実験を行い、色度座標を計算してグラフ化しました。
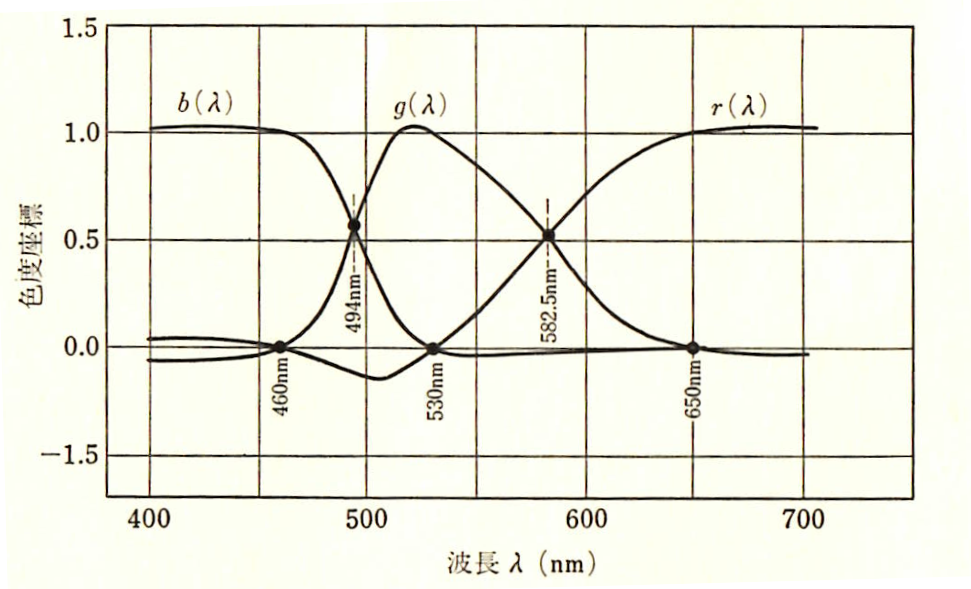
図-2.6 ライトの実験結果(池田光男 色彩工学の基礎 朝倉書店(1980))
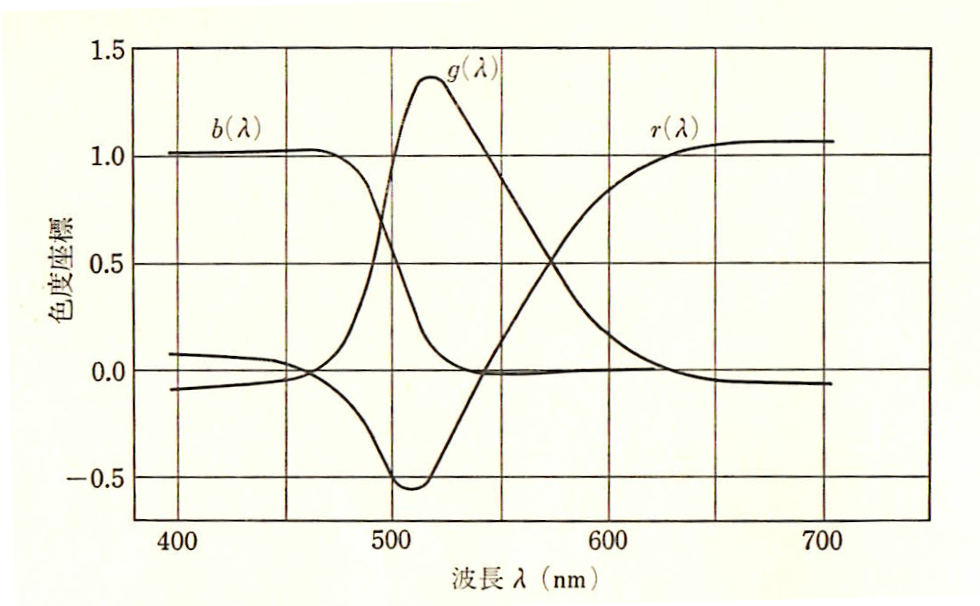
図-2.7 ギルドの実験結果(池田光男 色彩工学の基礎 朝倉書店(1980))
物理的に実在する器械原刺激として採用した650[nm]、530[nm]、460[nm]の所では
色度座標がそれぞれ(1,0,0)、(0,1,0)、(0,0,1)となります。また、582.5[nm]の波長では
r(λ)=g(λ)、494[nm]の波長ではg(λ)=b(λ)です。
すべての波長で r(λ) + g(λ) + b(λ) = 1 です。
原刺激以外の波長では、必ず3つの色度のうちどれか1つは負の値となっています。
これはどの単色光もその鮮やかさが、3つの原刺激をただ加え合わせたものよりも強い
ことを示しています。
特にその傾向は500[nm]近辺のシアンと呼ばれる青緑の領域で顕著です。
また、460[nm]以下、650[nm]以上の波長ではb(λ)あるいはr(λ)がほとんど1であり、
色の変化がそれほど見られません。
CIEによるRGB表色系の定義
ライトとギルドの実験結果からそれぞれ色度が得られました。原刺激の選び方や実験
装置が異なるため、同じ数値とはなりませんでしたが、CIEは計算によって2人の実験
データを同じ条件に揃え非常に近いことを確認し、信頼できるデータであると判断され
、最終的に、
原刺激は、700[nm]、546.1[nm]、435.8[nm]の3つの単色光に決められました。
そして、これら赤(R)、緑(G)、青(B)の原刺激を混色して等エネルギースペクトル白色
(すべての波長で等しいエネルギーを有する白色)と等色した時にそれらの三刺激値を
等しくする(R=G=B)ように定めました。
基礎刺激は等エネルギーの白色で、原刺激R、G、Bの明度係数lr、lg、lbは測光量の単位で
lr:lg:lb = 1:4.5907:0.0601 ・・・(2.10)
と決められました。
色度座標r(λ)、g(λ)、b(λ)はライトとギルドのデータを平均したデータが採用されました。
CIEが定めた色度座標 r(λ)、g(λ)、b(λ)のデータとグラフを以下に示します。
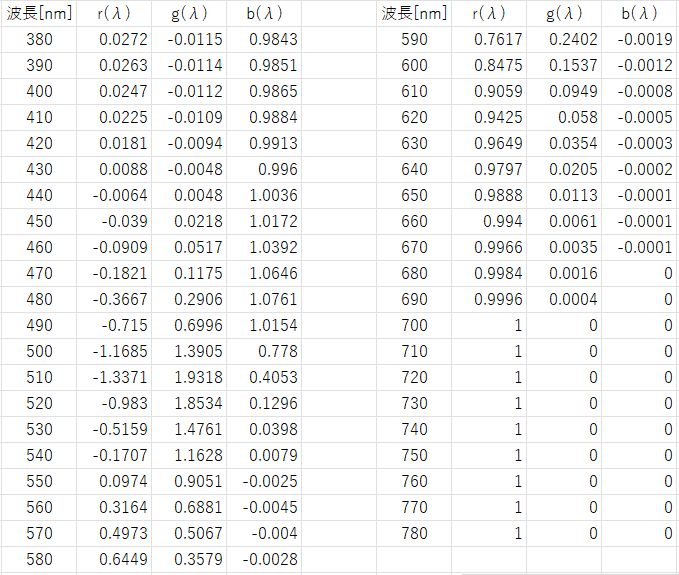
図-2.8 RGB色度座標データ(池田光男 色彩工学の基礎 朝倉書店(1980))
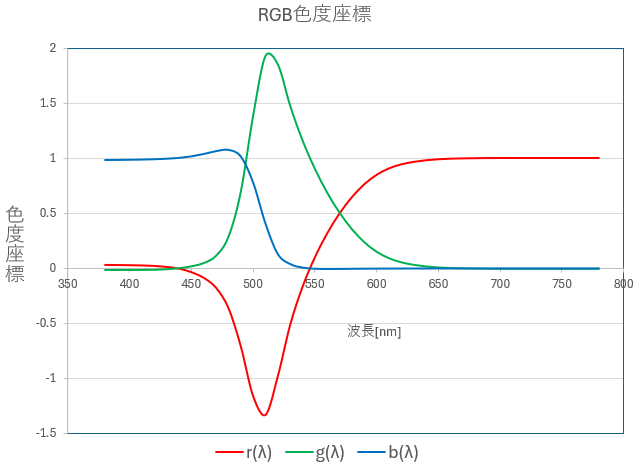
図-2.9 RGB色度座標グラフ
RGB色度座標の3次元表示
上記RGB色度座標を3次元表示すると図-2.10のようになります。
赤の平面はR=0、緑の平面はG=0、青の平面はB=0を表します。
赤い点は各波長における色度座標です。
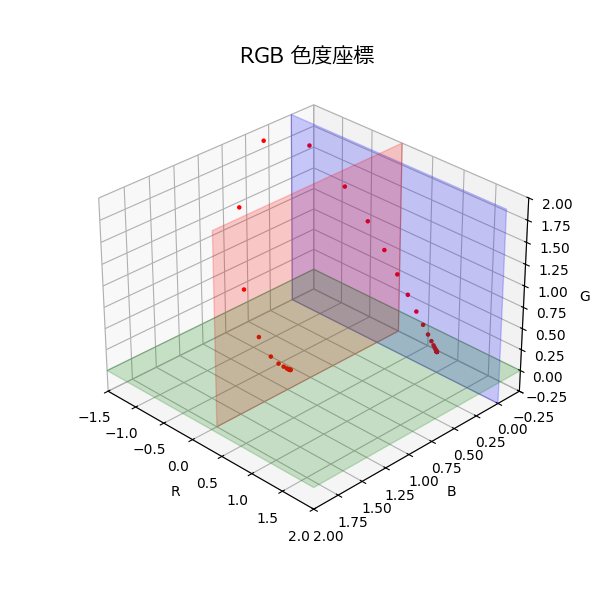
図-2.10 RGB色度座標3次元表示
この座標をRG面へ投影すると図-2.11になります。
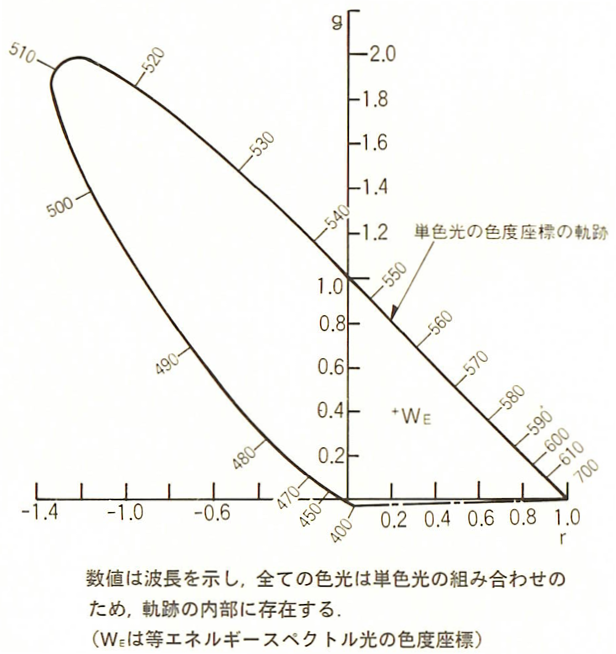
図-2.11 RG色度座標(池田光男 色彩工学の基礎 朝倉書店(1980))
等色関数
等色関数は、等エネルギースペクトルに対する原刺激の三刺激値
![]()
![]()
![]()
です。これを等色実験から直接測定するには単色光のエネルギーの測定が必要になりますが、
色度座標はR、G、Bの比が分かれば良いのでエネルギーの測定は必要ではありません。
ライトとギルドの等色実験でも色度座標を求めています。
色度座標から等色関数への変換は以下のように行います。
スペクトルの色度座標 をr(λ) g(λ) b(λ) とすると
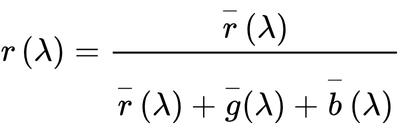 ・・・(2.15)
・・・(2.15)
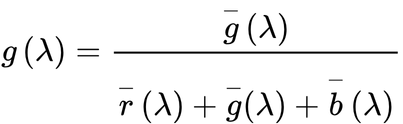 ・・・(2.16)
・・・(2.16)
![]() ・・・(2.17)
・・・(2.17)
で計算できます。
任意の色光Cの輝度Lcは式(2.4)の通り、
Lc = lrR + lgG + lbB ・・・(2.4)
です。また、等エネルギースペクトルの光束は分光視感効率V(λ)に比例しますので、比例定数を
1とした場合、式(2.4)より、
![]() ・・・(2.18)
・・・(2.18)
となります。
三刺激値は輝度を明度係数(lr,lg,lb)で割って作りましたので、式(2.18)は三刺激値に
明度係数を掛けることにより輝度が得られ、これが分光視感効率となります。
式(2.18)の両辺を
![]()
で割ると、
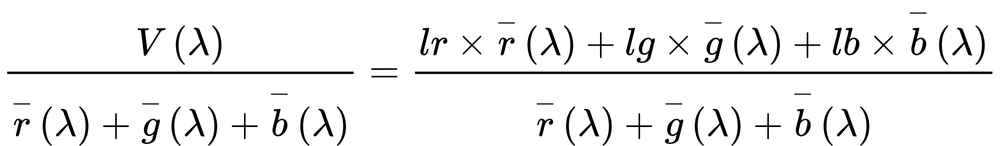 ・・・(2.19)
・・・(2.19)
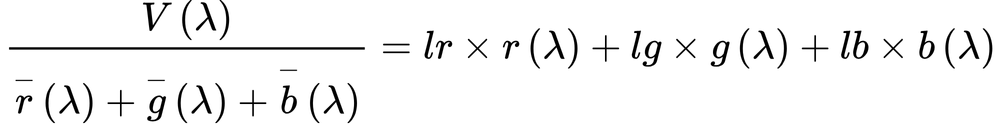 ・・・(2.20)
・・・(2.20)
(2.20)式より、
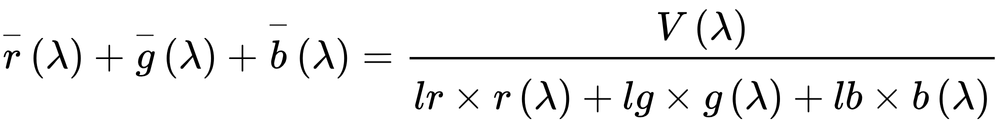 ・・・(2.21)
・・・(2.21)
となり、式(2.15)から式(2.17)の関係から
![]() ・・・(2.22)
・・・(2.22)
等を代入すると、
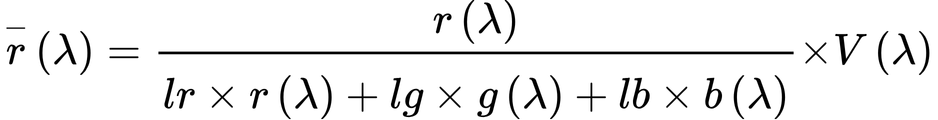 ・・・(2.23)
・・・(2.23)
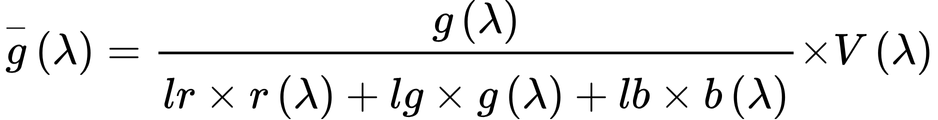 ・・・(2.24)
・・・(2.24)
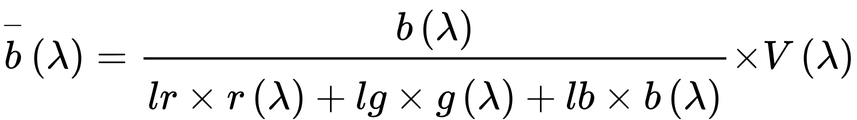 ・・・(2.25)
・・・(2.25)
となり、色度座標とV(λ)から等色関数が計算できます。
計算結果は以下の表になります。
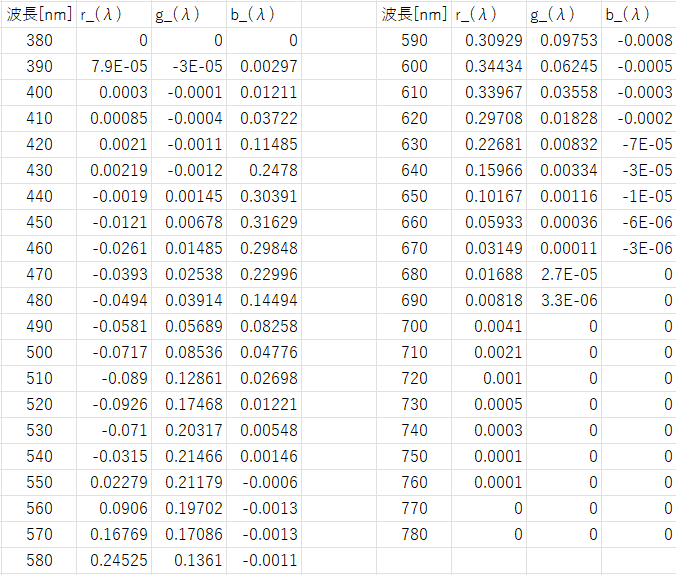
図-2.12 RGB等色関数データ(池田光男 色彩工学の基礎 朝倉書店(1980))
これをグラフにすると以下のようになります。
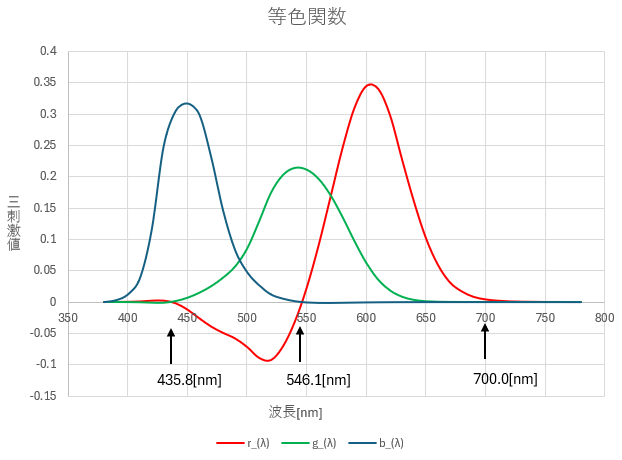
図-2.13 RGB等色関数グラフ
原刺激R(700.0[nm])の波長では、G=0、B=0です。
原刺激G(546.1[nm])の波長では、B=0、R=0です。
原刺激B(435.8[nm])の波長では、G=0、R=0です。
以下の(2.18)式
![]() ・・・(2.18)
・・・(2.18)
は、
lr = 1、 lg=4.5907、lb=0.0601
ですので、
![]() ・・・(2.19)
・・・(2.19)
ですから、これをそのまま計算すると、V(λ)そのものであることが
わかります。つまり、等エネルギースペクトルに対する原刺激の三刺激値に
それぞれの明度係数を掛けて加えたものがV(λ)になることを示しています。
式(2.19)の関係をグラフにすると図-2.14になります。
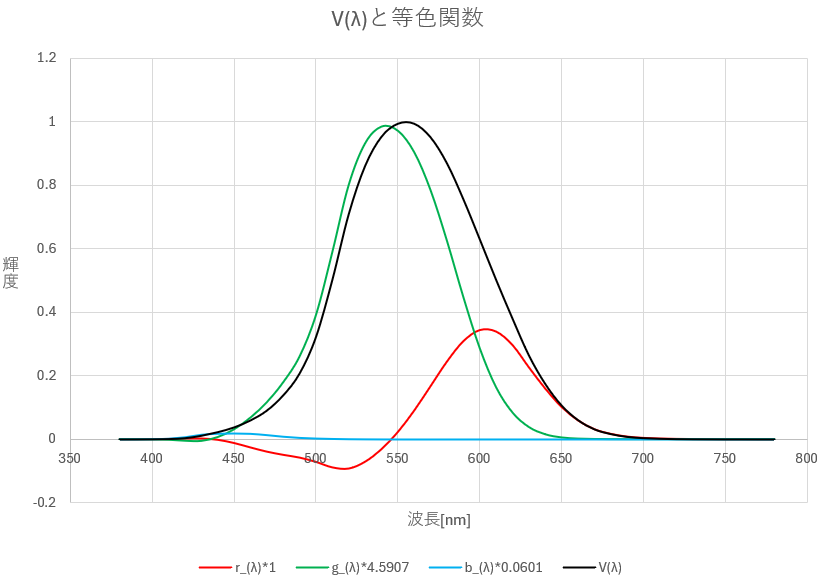
図-2.14 RGB等色関数とV(λ)
RGB表色系を用いれば色を三刺激値で表現できますが、負の三刺激値が存在するなどの
問題点があり、これらを解決するためにXYZ表色系が制定されました。