RGB表色系を用いれば色を三刺激値で表現できます。しかしながらこの表色系には
欠点があり、特に次の2点が問題になります。
1.負の三刺激値がある。
2.輝度を表現する場合、以下の式で変換する必要がある。
Lc = R + 4.5907G + 0.0601B ・・・RGB表色系の(2.4)
これらの点を解決するためにXYZ表色系が制定されました。
1.の問題を解決するために、図のスペクトル軌跡をすべて含む3角形の頂点に色度
座標を持つような原刺激(X)(Y)(Z)を用いました。しかしこのような色刺激は実際には
存在しないため虚色と呼ばれます。
2.の問題についてはRGB表色系の式(2.4)のLc=0、つまり
R + 4.5907G + 0.0601B = 0 ・・・(3.1)
を考えます。
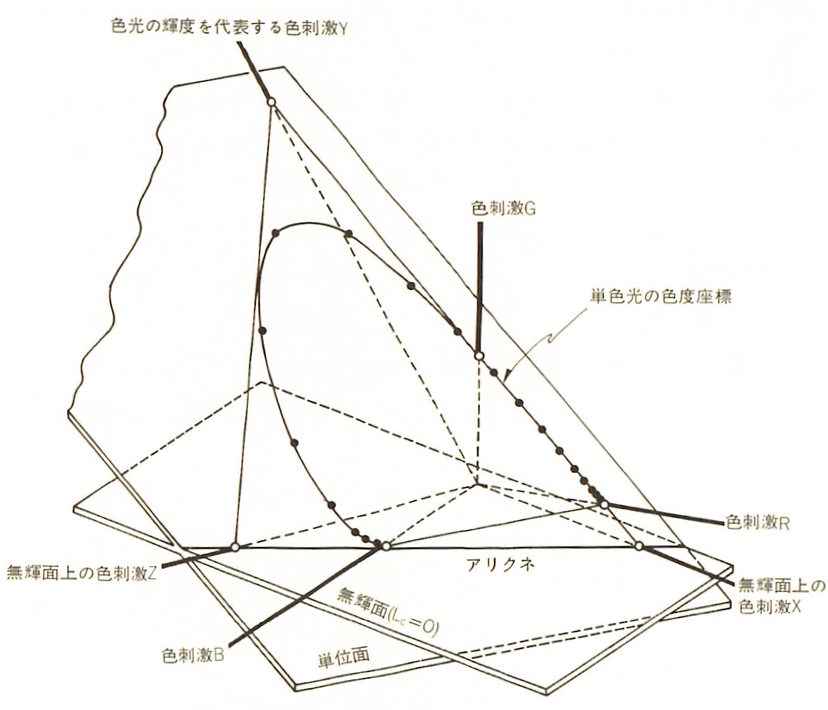
図-3.1 RGB表色系の単位面と無輝面との位置関係
(池田光男 色彩工学の基礎 朝倉書店(1980))
これは原点を通る平面の式で、Lc=0で輝度が0ですので、無輝面と呼ばれます。
無輝面と単位面の交線はアリクネ(alycne)と呼ばれ、2次元の色度図上にも直線
として表示されます。輝度がゼロの直線なので、無輝線です。
式(3.1)に R+G+B=1を代入し、Rをr、Gをgと書き換えて整理すると
0.9399r + 4.5306g + 0.0601 = 0 ・・・(3.2)
が得られます。これが無輝線の式です。
原刺激(X)(Y)(Z)のうち(X)と(Z)を無輝面上にとることにより、それらの原刺激の
輝度は0になります。明度係数をlx、ly、lzとすれば色光Cの輝度Lcは
Lc = lxX + lyY + lzZ ・・・(3.3)
となるため、
XYZ表色系での輝度は
Lc = lyY ・・・(3.4)
となります。三刺激値のうちYだけを知れば輝度が求められることになります。
式(3.3)は、以下のRGB表色系の式(2.4)に相当するものであり、
Lc = lrR + lgG + lbB ・・・(2.4)
X、Y、ZはXYZ座標系で色光Cを表した時の三刺激値です。
C(C) ≡ X(X) + Y(Y) + Z(Z) ・・・(3.5)
が成立します。また、XYZ表色系の等色関数を
![]()
とすると、以下のRGB表色系の式(2.18)
![]() ・・・(2.18)
・・・(2.18)
に対応して
![]() ・・・(3.6)
・・・(3.6)
が成立し、lx = 0、 ly = 0ですので、
![]() ・・・(3.7)
・・・(3.7)
となり、XYZ表色系の等色関数のうち、
![]()
は標準分光視感効率(比視感度)と一致します。
このようにしてXYZ表色系の原刺激が定められました。これを図-(3.2)と式(3.8)に
示します。
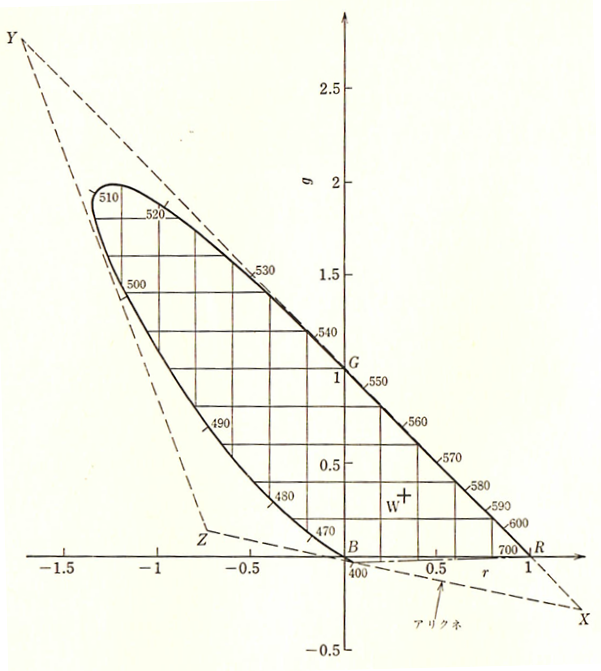
図-3.2 RGB表色系のRG色度図上のXYZ表色系の原刺激X、Y、Zの位置
(池田光男 色彩工学の基礎 朝倉書店(1980))
XとZは式(3.2)で示されるアリクネの上にとり、XとYを結ぶ線は700[nm]~560[nm]
のスペクトル軌跡を延長してできる直線上にあります。YとZを結ぶ線は504[nm]の波長の
ところでスペクトル軌跡にほぼ接するように決まりました。
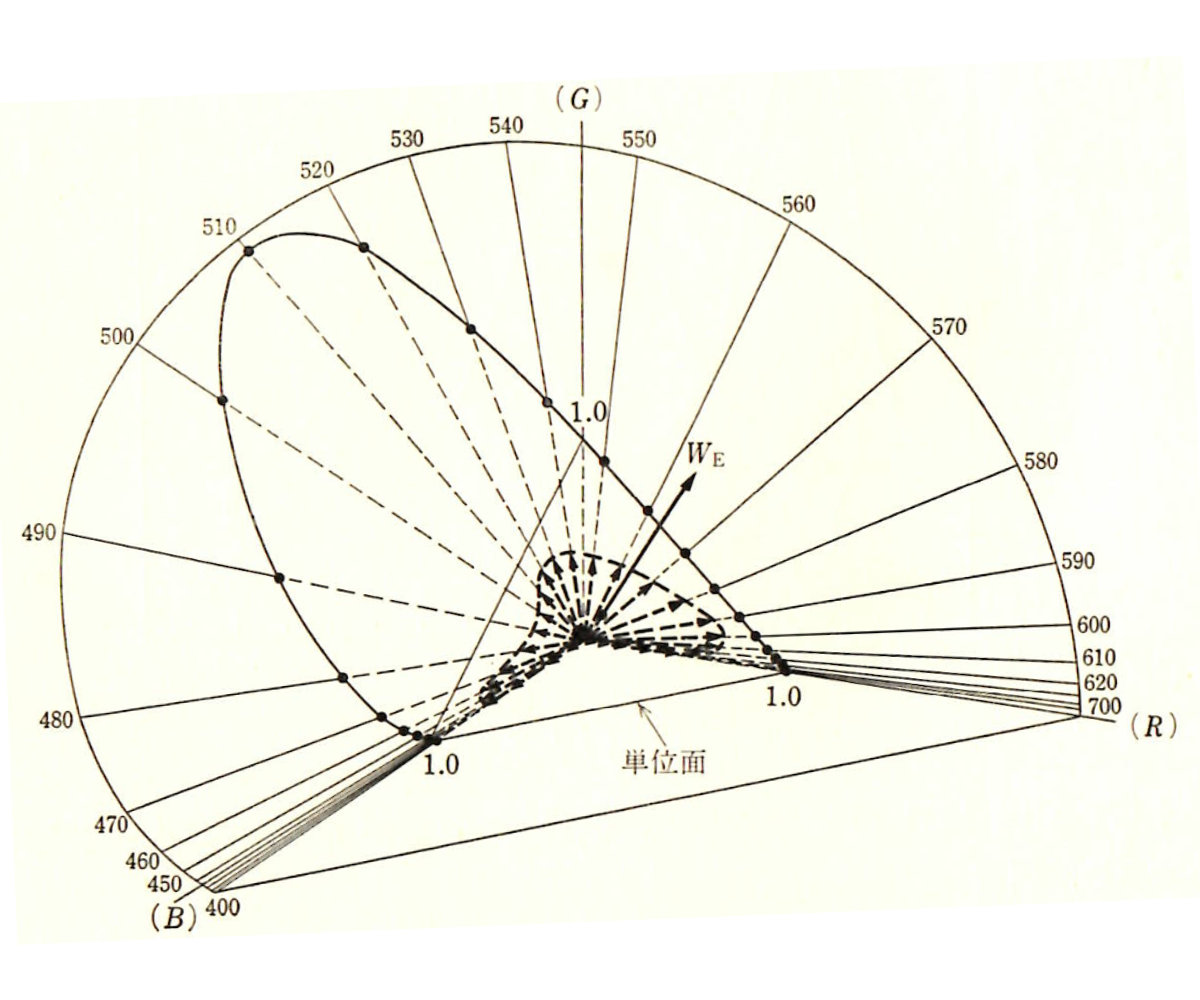
図-3.3 RGB表色系三次元色度座標と等エネルギースペクトル
(池田光男 色彩工学の基礎 朝倉書店(1980))
矢印は等エネルギースペクトル(長さは実際の2倍で表示)
(矢印の先端の座標は等色関数の座標)
Weは等エネルギー白色
黒点を結ぶ曲線は色度図におけるスペクトル軌跡
XYZ表色系の原刺激の(r,g,b)色度座標は以下の通りです。
X(1.2750, -0,2778, 0.0028)
Y(-1.7392, 2.7671, -0.0279) ・・・(3.8)
Z(-0.7431, 0.1409, 1.6022)
RGB表色系からXYZ表色系への変換
ある色光CはRGB表色系の三刺激値R、G、Bによって表されます。
C(C) ≡ R(R) + G(G) + B(B) ・・・(3.9)
また、式(3.5)より
C(C) ≡ X(X) + Y(Y) + Z(Z) ・・・(3.5)
であるので、色光Cの三刺激値R、G、Bが与えられたとき、X、Y、Zについて
次の式が成り立ちます。
X = XrR + XgG + XbB
Y = YrR + YgG + YbB ・・・(3.10)
Z = ZrR + ZgG + ZbB
式(3.10)の係数Xr~Zbの9個の係数を求めれば変換ができます。
色光CがX軸と一致するときは、Y = Z = 0であるので、この時のR、G、Bの値
は式(3.8)のXの座標で与えられています。従って、
1.2750Yr – 0.2778Yg + 0.0028Yb = 0 ・・・(3.11)
1.2750Zr – 0.2778Zg + 0.0028Zb = 0
となります。同様にCがY軸と一致するときとZ軸と一致するときは
-1.7392Xr + 2.7671Xg – 0.0279Xb = 0
-1.7392Zr + 2.7671Zg – 0.0279Zb = 0 ・・・(3.12)
-0.7431Xr + 0.1409Xg +1.6022Xb = 0
-0.7431Yr + 0.1409Yg +1.6022Yb = 0
です。
次の条件としてCが等エネルギー白色の場合、R=G=B、X=Y=Zですので、
Xr + Xg + Xb = Yr + Yg + Yb = Zr + Zg + Zb ・・・(3.13)
が成立します。さらにYを輝度と一致させるため、下記式(2.4)
Lc = R + 4.5907G + 0.0601B ・・・RGB表色系の(2.4)
の明度係数の関係から、
Yr + Yg + Yb = lr + lg + lb = 1 + 4.5907 + 0.0601 = 5.6508 ・・・(3.14)
となります。式(3.11)、式(3.12)、式3.13)、式(3.14)より、
Xr = 2.7689, Xg = 1.7517, Xb = 1.1302
Yr = 1.0000, Yg = 4.5907, Yb = 0.0601 ・・・(3.15)
Zr = 0.0000, Zg = 0.0565, Zb = 5.5943
が得られます。これらを式(3.10)に代入すると
X = 2.7689R + 1.7517G + 1.1302B
Y = 1.0000R + 4.5907G + 0.0601B ・・・(3.16)
Z = 0.0000R + 0.0565G + 5.5943B
となります。
これから色度座標x、y、zを求めるには、以下の式(3.17)に式(3.16)を代入して
x = X / (X + Y + Z)
y = Y / (X + Y + Z) ・・・(3.17)
z = Z / (X + Y + Z)
以下の式が得られます。
x = (2.7689R + 1.7517G + 1.1302B) / (3.7689R + 6.3989G + 6.7846B)
y = (1.0000R + 4.5907G + 0.0601B) / (3.7689R + 6.3989G + 6.7846B) ・・・(3.18)
z = (0.0000R + 0.0565G + 5.5943B) / (3.7689R + 6.3989G + 6.7846B)
ここで、RGBの色度座標の式
r = R / (R + G + B)
g = G / (R + G + B) ・・・(3.19)
b = B / (R + G + B)
を、以下のように変形して
R = r(R + G + B)
G = g(R + G + B) ・・・(3.20)
B = b(R + G + B)
とし、式(3.18)に代入して最終的に
x = (2.7689r + 1.7517g + 1.1302b) / (3.7689r + 6.3989g + 6.7846b)
y = (1.0000r + 4.5907g + 0.0601b) / (3.7689r + 6.3989g + 6.7846b) ・・・(3.29)
z = (0.0000r + 0.0565g + 5.5943b) / (3.7689r + 6.3989g+ 6.7846b)
が得られます。
これにRGB表色系の色度座標を代入してXYZ表色系の色度座標x(λ)、y(λ)、z(λ)
を求めると以下の表のようになります。
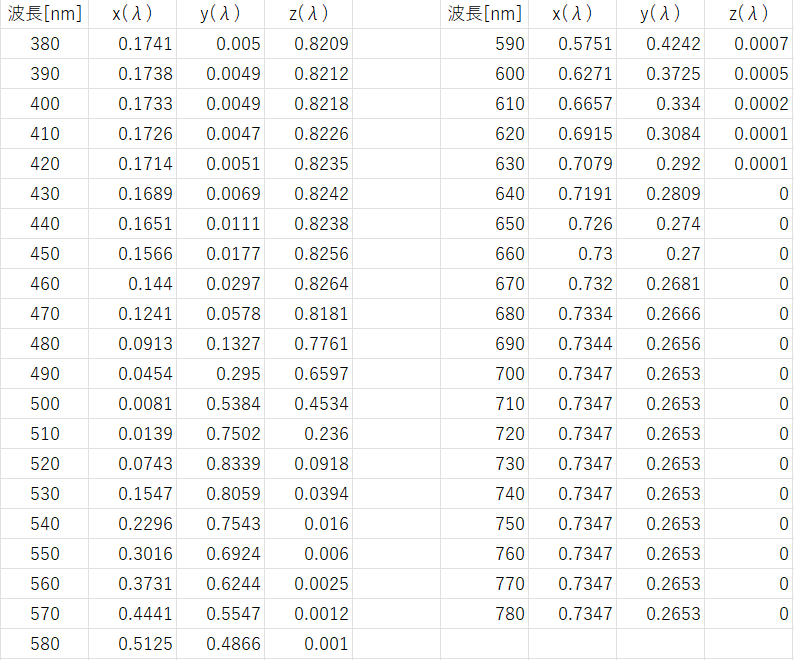
図-3.5 XYZ表色系の色度座標
XYZ表色系の等色関数は色度座標から以下のように求められます。
x_(λ)、y_(λ)、z_(λ)を等色関数とします。
x_(λ) = ( x(λ) / y(λ) ) V(λ)
y_(λ) = V(λ) ・・・(3.30)
z_(λ) = ( z(λ) / y(λ) ) V(λ)
式(3.30)により計算すると以下の表のようになります。
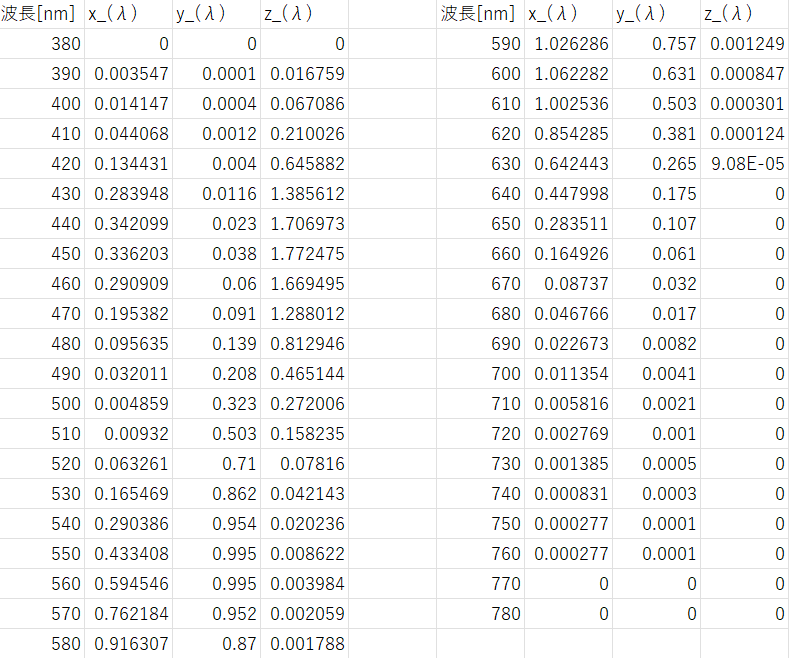
図-3.6 XYZ表色系の等色関数
これをグラフに表示すると図-3.7になります。
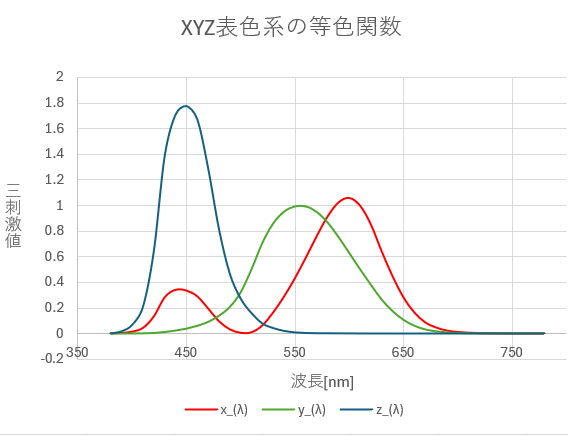
図-3.7 XYZ表色系の等色関数のグラフ
図-3.5 XYZ表色系の色度座標のデータを3次元表示すると図-3.8の
XYZ表色系色度座標の3次元表示グラフとなります。
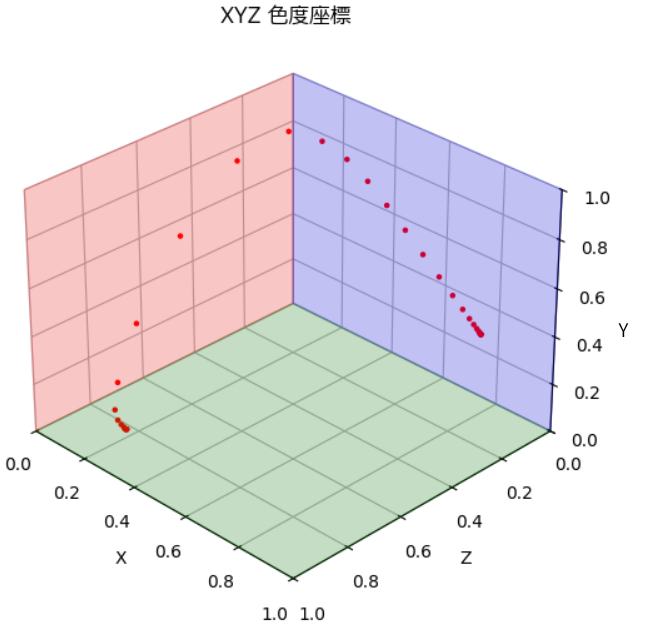
図-3.8 XYZ表色系色度座標の3次元表示グラフ
図-3.8のXYZ表色系色度座標の3次元表示グラフをXY平面に投影しxy色度図としてプロット
すると図-3.9のxy色度図になります。
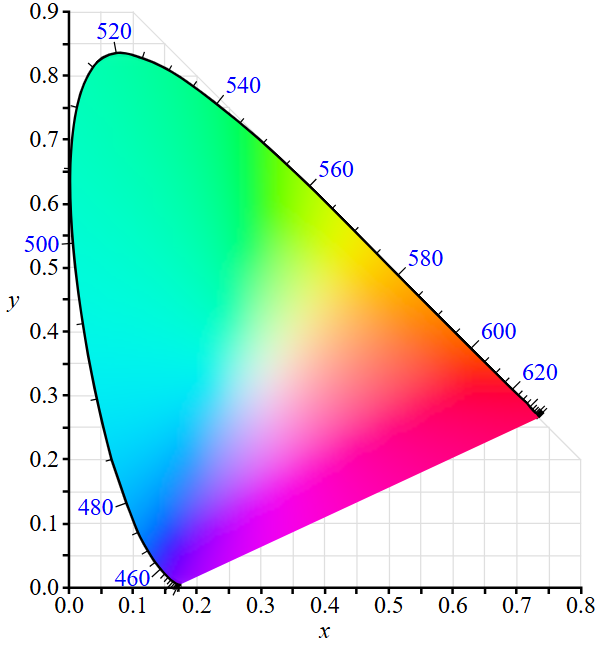
図-3.9 xy色度図(CIE 1931 color space – Wikipediaより)
等色関数を使って等エネルギースペクトルを3次元表示すると図-3.10の矢印
のようになります。矢印と単位面との交点が色度座標で、この色度座標をXY平面
に投影したものが図-3.9のxy色度図です。
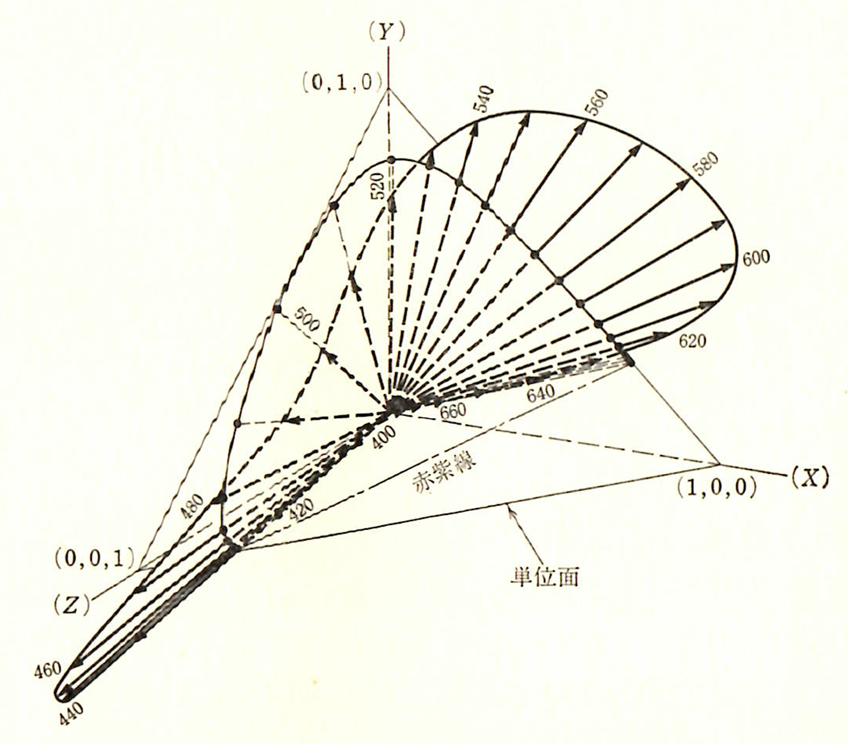
図-3.10 XYZ表色系三次元色度座標と等エネルギースペクトル
(池田光男 色彩工学の基礎 朝倉書店(1980))
矢印は等エネルギースペクトル。黒点を結ぶ曲線は
色度図のスペクトル軌跡を表します。
次は色々な分光分布から色度座標を求めます。